# 0. Abstract
- Nested queries that are correlated with the outer queries frequently lead to dependent joins with nested loops evaluations and thus poor performance.
- 现有系统使用启发式规则来进行 unnest,缺陷是不通用,仅仅能处理某些确定类型的查询。
-------
# 1. Introduction
- schemas:
- **students**: `{[id, name, major, year, . . . ]} `
- **exams**: `{[sid, course, curriculum, date, . . . ]}`
- **Q1**:查找每个学生的 best exams(按照德国评分系统,分数越低越好)
```sql
select s.name,e.course
from students s,exams e
where s.id=e.sid and
e.grade=(select min(e2.grade) from exams e2 where s.id=e2.sid)
```
- 性能不好:对于每个 student 都需要计算一次子查询
- 这个查询包含了一个 dependent join:
- a nested loop join where the evaluation of the right hand side depends on the current value of the left-hand side.
- 这类 join 非常不高效,导致 quadratic execution time(至少)。
- DBMSs 因此在内部会将查询重写,将 Q1 去关联:
```sql
-- Q1‘
select s.name,e.course
from
students s,
exams e,
(select e2.sid as id, min(e2.grade) as best
from exams e2 group by e2.sid) m
where s.id=e.sid and
m.id=s.id and
e.grade=m.best
```
- 重写后 subquery 的计算不再依赖 s 中的 values,因此可以使用普通的 joins。
- **Q2**:没有任何现有系统可以去关联 Q2
```SQL
select s.name, e.course
from students s, exams e
where s.id=e.sid and
(s.major = ’CS’ or s.major = ’Games Eng’) and
e.grade>=(select avg(e2.grade)+1 --one grade worse
from exams e2 --than the average grade
where s.id=e2.sid or --of exams taken by
(e2.curriculum=s.major and --him/her or taken
s.year>e2.date)) --by elder peers
```
> We will have to spend extra effort to derive the value of `s.year` and `s.major`, but we can do so without a dependent join.
- 我们的 unnesting 方式不会比 straightforward nested loops evaluation 更差,并且大多数情况下能有效提升性能(通常是几个数量级)
- 另外消除 dependent joins 后,使得更高效的 join 实现成为可能。
- 在线体验:[hyper web interface](https://hyper-db.de/interface.html#)
- 去关联的性能收益是巨大的:
- 取决于具体的查询,将 $O(n^2)$ 的 nested loop join 算法替换为 $O(n)$ 的算法(hash join,joining keys)。
- 此外,the dependent side is executed for every outer tuple in the nested case, but only once in the unnested case.
- nested 形式有优势的场景:
- outer side 很小,inner side 计算时可以使用 index loop up
- 但这应该是由查询优化器的主动决定触发,而不是根据查询的形式
- **默认查询应该完全被 unnested**
-----
# 2. Preliminaries
- Inner join 定义为 cross product 加 selection
- $\large T_1 \bowtie_p T_2 := \sigma_p(T_1 \times T_2)$
- 不适用于存在关联子查询的情况:子查询必须根据 outer query 中的每个 tuple 进行求值。
- 因此将 **dpendent join** 定义为:
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_dpendent_def.png" width='500'>
- 对于左边的每一个 tuple 都会计算一次右边
- 将表达式 T 的输出的 attributes 标记为 ${\mathcal{A}}(T)$
- 将表达式 T 中出现自由变量(free variables)标记为 ${\mathcal{F}}(T)$
- 为了计算 dependent join,${\mathcal{F}}(T_2) \subseteq {\mathcal{A}}(T_1)$ 必须成立,即 $T_2$ 需要的 attributes 必须由 $T_1$ 产生。
- 我们假设查询中出现的所有关系都具有唯一的 attribute names,即时它们指向相同的 physical table,因此 $A \bowtie B ≡ A \times B$ 。(natural join 会消除同名的列,这里列都不相同)。
- 但是如果我们**显式地引用**相同的 relation name 两次,然后调用 natural join,那么会比较相同名字的 attribute columns,然后重复 columns 会被 projected out。
- 例如 $\large (A \bowtie C) \bowtie_{p \wedge \ natural \ join \ c}(B \bowtie C)$
- 最顶层的 join 会检查谓词 p 并且比较两边来自 C 的 columns(消除 C 的重复列)
- 除了 join operators,我们还有 *group by* operators作为额外重要的 operator
- $\large \begin{array}{r l}{\mathcal{G}_{A;a:f}(e)}&{{}:=}&{{}\{x\circ(a:f(y))|x\in\Pi_{A}(e)\land y=\{z|z\in e\land\forall a\in A:x.a=z.a\}\}}\end{array}$
- 按照 A 对输入 e 进行分组,然后计算一到多个聚合函数来计算聚合后的 attributes。
- 如果 A 为空,只输出一个 aggragation tuple(即不带 group by 子句)
- 通过计算 *map* operator 来计算函数(并且因此创建出新的 attributes)
- $\large \begin{array}{r l}{\mathcal{X}_{a:f}(e)}&{{}:=}&{{}\{x\circ(a:f(x))|x\in e}\}\end{array}$
- 我们经常需要比较一组 attriutes,将 attribute comparsion operator $=_{A}$ 定义为:
- $\large t_{1}=_{A}t_{2}\quad:=\quad\forall_{a\in A}:t_{1}.a=t_{2}.a.$
- 请注意,除非另有说明,否则此运算符具有 is sementics,即以相等来比较 NULL 值。
-------
# 3. Unnest
- 两种技术:
- **simple unnesting**:
- 处理仅仅因为语法原因创建依赖的场景
- dependencies are created just for syntactic reasons
- **general unnesting**:
- 处理任意复杂的查询
## 3.1 Simple Unnesting
- 有时候查询包含关联子查询只是因为它们容易在 SQL 中表达:
```SQL
select ...
from lineitem l1 ...
where exists (select * from lineitem l2 where l2.l_orderkey = l1.l_orderkey) ...
```
- 转换成关系表达式的形式:
- 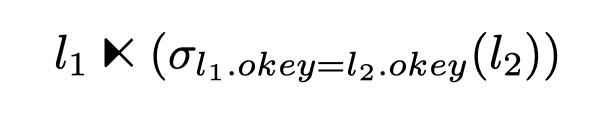
- 通过将 dependent predicate 往上移动,将其转换为普通 join
- 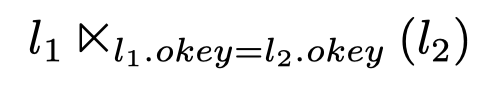
- semi join
- simple unnesting 将所有 dependent predicates 尽可能地往上移动,可能会越过 joins,selections,group by等等,直到它的所有 attributes 都可以从 input 中获取。
> In general the simple unnesting phase moves all dependent predicates up the algebra tree as far as possible, potentially beyond joins, selections, group by, etc., until it reaches a point where all its attributes are available from the input.
- 这种上移只是为了去除关联,后续的优化可能会将部分谓词再下推回去。
## 3.2 Genernal Unnesting
- predicate movement 很容易实现,并且足够处理经常出现的简单嵌套查询。
- 通用场景需要更复杂的方式:
1. 将 dependent join 转换成 nicer dependent join(更容易操作的)
2. push new dependent join down into the query,直到可以将它转换成普通的 join
- 在第一步中,我们使用以下的等价性:
- <img src='https://img.jonahgao.com/oss/note/2025p1/unnest_general_equal.png' width='350'>
- 其中 $\large {\cal D}\quad:=\quad \Pi_{{\mathcal F}(T_{2}){\cap}{\mathcal A}(T_1)}(T_1)$
- 原始表达式中,对于 $T_1$ 的每个 tuple 都要计算 $T_2$,可能会几百万次
- 右边的表达式中,我们先计算所有 variable bindings 的 domain D,只对每一个 distinct variable binding 计算 $T_2$ ,然后使用普通 join 来匹配 $T_1$ 中的原始结果。如果重复度很高,就能极大得减少对 $T_2$ 的计算。
- **Example**:
- 原始:
- <img src='https://img.jonahgao.com/oss/note/2025p1/unnest_example_01.png' width='500'>
- 利用等价式可以将为每个 (student, exam) 对计算 best grade 转变为对每个 student 计算 best grade:
- <img src='https://img.jonahgao.com/oss/note/2025p1/unnest_example_02.png' width='500'>
- 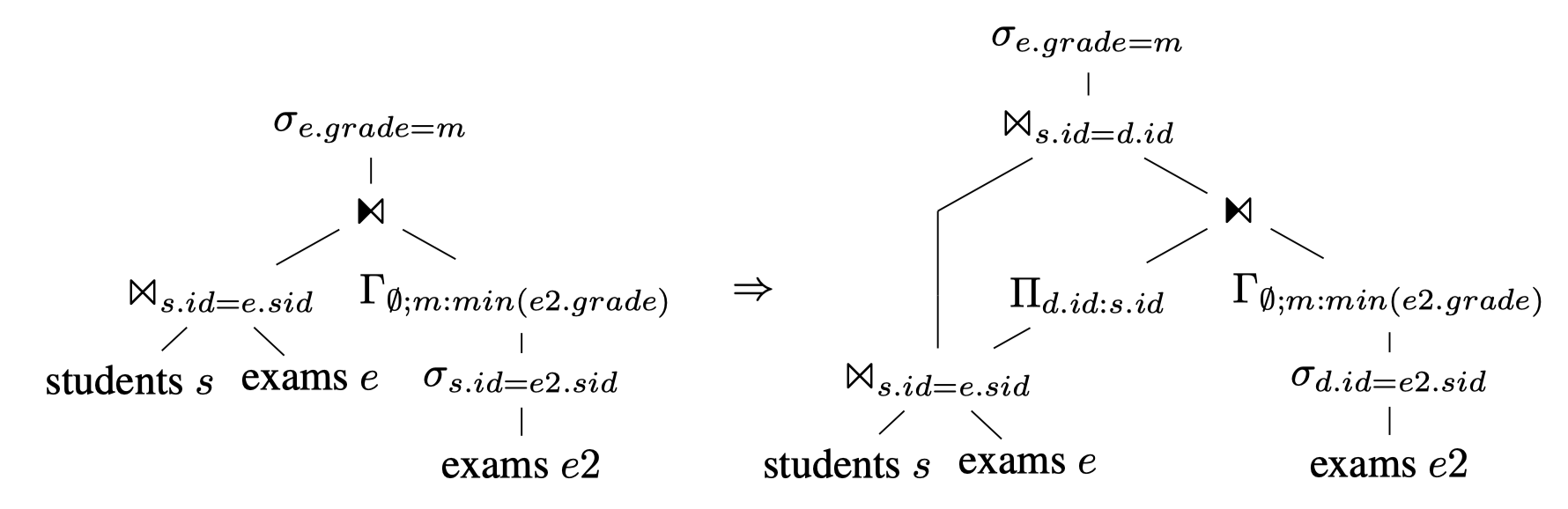
- In a way, this constitutes a **side-ways information passing** from the outer (left) join argument to the inner (right) argument in order to eliminate redundancy in the evaluation.
- 我们将 generic dependent join 转换成了 dependent join of a *set*(没有重复),${\cal D}$ 没有重复有助于进一步地将 dependent join move down 到 query 中。接下来我们都将假设名为 ${\cal D}$ 的 relation 消除了重复。
- depdent join push-down 的终极目标就是达到一个状态:右边不再依赖左边
- <img src='https://img.jonahgao.com/oss/note/2025p1/unnest_push_down.png' width='400'>
- 这种场景下,仍然需要执行一次 join,但已经不是低效的 dependent join。
- 我们将会看到,我们总是可以达到这个状态。
- 一种更好的目标是当达到这种状态是,产生的普通 join 可以使用已有的 attributes 替代,从而也一起消除最后的 join。(将在第四章讨论)
<br>
- 在解释了 dependent join push down 的起始和目标后,我们来看看单独的 operators。
### pushdown selection
- selection 的 push down 很简单:
- <img src='https://img.jonahgao.com/oss/note/2025p1/unnest_selection_push.png' width='300'>
- 这个转换看起来不太寻常,跟传统的 selection push down 不一样
- 但是我们要做的是先尽可能地将 dependent join push down,知道到达终极目标。
- 之后再执行传统的 selection push-down 和 join reordering 。
### pushdown join
- 将一个 dependent join pushdown 到另一个 join 更复杂,因为两边可能都依赖 dependent join。
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_join_push.png" width="800" />
- 这个下推规则是过于悲观的,我们通常可以简化 join 下面的部分(见第四章)
- 如果我们将 dependent join 下推到两边,我们必须增加 join predicate,使两边在 D 的 values 上匹配。这里的重复相比原来的表达式并不会损失性能,两种情况 $T_1$ 和 $T_2$ 都需要计算 $|D|$ 次。
- 对于 outer joins 我们需要始终 replicate the dependent join 如果 inner side 依赖它,否则我们就无法从 outer side 跟踪 unmatched tuples
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_join_push2.png" width="800" />
- semi join 和 anti join 也类似:
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_join_push3.png" width="800" />
### pushdown group-by
- 当下推 dependent join 到 group-by operator 时,group-operator 必须保留 dependent join 输出的所有属性。
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_groupby_push.png" width="400" />
### pushdown projection
- projection 的行为类似 group by operator
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_projection_push.png" width="350" />
### set operators
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_set_push.png" width="360"/>
### summary
- 使用这些转换,每个 dependent join 要不在某处被消除,要不就是在 base relation 前结束,这种情况它可以被转换成一个 non-dependent join。因此可以消除任何查询中的 dependent join。
- 另外一个潜在的风险是 D 可能很大,它是 nested subquery 中所有 variable bindings 的集合。但实际上并非如此:
- 如果原始的 nested join 是 $T_1$ depedent join $T_2$,那么 $|D| \leq |T_1|$,因此去关联后如果 top-most join 是一个 hash join(存储 $T_1$ 在一个 hash table 中),则 join 的内存消耗最多是计算 D 的两倍( D 跟 $T1$ 大小相同,多了一次 join),这还是最坏的情况。
- 如果知道 $T_1$ 没有重复(比如是主键),我们甚至可以避免物化 D,而是直接读取 join hash table,去除任何额外开销。
- 另外我们将一个 $O(n^2)$ 的操作理想状况下转换成 $O(n)$操作,多余的内存开销是值得的
## 3.3 Optimization of Example Query Q1
```sql
select s.name,e.course
from students s,exams e
where s.id=e.sid and
e.grade=(select min(e2.grade) from exams e2 where s.id=e2.sid)
```
<img src="https://img.jonahgao.com/oss/note/2025p1/unnest_query1_1.png" width="400"/>
<img src="https://img.jonahgao.com/oss/note/2025p1/unnest_query1_2.png" width="500"/>
- 在许多场景中(例如本例子),可以消除与domain D 的 join。
- 如果 domain 的所有属性都 (equi-)joined with 已有的属性,我们可以从已有的属性派生出 domain
- 本例子中,我们知道 join 后 $d.id = e2.sid$ 仍有成立,因此可以像下图一样替换为一个 map operator(将 $d.id$ 替换成 $e2.sid$)
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_query1_3.png" width="600" />
- 但是替换可能会创建出原本 tuples 的 superset,可能会导致中间结果很大
- 不影响最终结果,后续还会有一个 filter
- 但是会影响 query runtime,是否移除这个 join 需要由 query optimizer 来决定。
- 替换后,尝试移除 $\large \sigma_{d.id=e2.sid}$ 时需要小心。只有当 $e2.sid$ 是 non-nullable 时才安全。否则 该 selection 必须保留(实际上只是一个 NOT NULL 检测)。
## 3.4 Optimization of Example Query Q2
```SQL
select s.name, e.course
from students s, exams e
where s.id=e.sid and
(s.major = ’CS’ or s.major = ’Games Eng’) and
e.grade>=(select avg(e2.grade)+1 --one grade worse
from exams e2 --than the average grade
where s.id=e2.sid or --of exams taken by
(e2.curriculum=s.major and --him/her or taken
s.year>e2.date)) --by elder peers
```
<img src="https://img.jonahgao.com/oss/note/2025p1/unnest_query2_1.png" width="800" />
- 这里的 D 不能被消除,因为有来自 D values 的 non-equi join
## 3.5 Anti-Join Example
- dpendent anti-join,用来转换 SQL all-clause(将一个 value 与可能关联的子查询输出的所有 values 比较)
- Q3:
```sql
select R.* from R
where R.X = all (select S.Y from S where S.B = R.A)
```
- 无法将查询转换成 dependent join,但是可能来 negate the predicate,然后使用一个 depdentent anti join。depdentent anti join 可以转换成普通 anti-join。
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_query3.png" width="600" />
-----------
# 4. Optimizations
- neral unnesting 必须添加 projection 来计算 domain D,然后跟 D 做 join,带来额外的开销。
- 通常来说,如果我们可以使用 sbutree 中已经存在的 values 替换 D,则可以消除 D。
- 最常见的是 equi-joins,$D \bowtie_{D.a=R.b} R$,we can learn the possible values of D.a that can make it to the original dependent join by inspecting the values of R.b.
- D 可能包含了 R 中不存在的 values,但是不会找到一个 join partner,因此不会达到原始的 dependent join,因此可以忽略它们
- 为了决策替换,我们必须首先分析 query tree 来找到由 join 和 filter 条件引起的等价类。
- 例如 $\sigma_{a = b}$ 暗示了 a 和 b 是相同的等价类,因此可以替换 a 为 b
- 可能存在异常情况的是 ouer joins,会导致 a 和 b 不想等, 但是 top-most join on D 已知是 NULL-regjecting,因此在这里不是问题。
- 当识别出等价类 C 后,我们可以实施如下替换
- <img src="https://img.jonahgao.com/oss/note/2025p1/unnest_opt_replace.png" width="500" />
- 因此我们可以扩展 T (使用 map operaotr),使用等价的属性计算 D 中的隐含属性。
- **NOTE**:这只适合 D 是一个 set 的情况
- **NOTE**:可能会增加中间结果的大小,公式中的关系是子集而非相等
- 但 original dependent join 被执行时,没有 join partner 的 tuples 会被消除(higher up in the tree)
- substitution only pays off if the join with D is unselective(Q1 属于这种情况)
- 查询优化需要比较两者的开销,选择 cost 低的那个。
- 对于 selective joins,最好是保留 D,可以尽早 eliminate tuples。
-----
# 6. Related Work
- [ ] 阅读提及的其他论文